머신러닝 입문 / 회귀분석 / 미분 / 경사하강법 / 지역 최소값 문제

 

 

 

 

머신러닝을 처음 배우면 가장 먼저 마주하는 개념 중 하나가 회귀분석(Regression Analysis) 입니다. 데이터를 이용해 최적의 예측 모델을 찾는 과정입니다. 이때 중요한 도구가 미분(도함수) 그리고 경사하강법(Gradient Descent) 입니다.

오늘은 이에 대해 자세히 살펴보겠습니다.

 

1. 함수와 그래프, 그리고 기울기

먼저 간단한 함수 $f(x) = x^2$ 를 생각해볼게요. 이 함수는 아래처럼 U자 형태의 그래프를 가집니다.

import numpy as np
import matplotlib.pyplot as plt

def my_f(x):
    return x**2

sample = np.linspace(-10, 10, 100)
f_x = my_f(sample)

plt.plot(sample, f_x, label='f(x) = x²', color='blue')
plt.title('f(x) = x² 그래프')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid(True)
plt.legend()
plt.show()

이 곡선에서 특정 점에서의 기울기를 알고 싶을 때, 미분을 사용합니다.

---

2. 미분이란 무엇인가?

미분은 말 그대로, 변화율(기울기) 를 나타냅니다.

$$ f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} $$

예를 들어, $f(x)=x^2$ 일 때,

$ f'(x) = 2x $ 가 됩니다.

👉 이렇게 미분을 하면, 함수의 최솟값 또는 최댓값을 찾는 데 활용할 수 있습니다. 특히, 기울기가 0이 되는 지점이 극값입니다!

---

3. 경사하강법이란?

경사하강법(Gradient Descent) 은 말 그대로 기울기를 따라 조금씩 내려가며 함수의 최소값을 찾는 방법입니다.

직관적으로, 공을 언덕 위에 올려놓으면 기울기가 있는 방향으로 굴러서 낮은 곳(최솟값)으로 이동하죠?
이 원리를 수학적으로 구현한 게 경사하강법입니다.

---

4. 실습: 평균을 경사하강법으로 찾아보기

📌 평균을 직접 계산하는 대신, 기울기를 따라 움직이면서 평균을 찾아보자!

x = np.array([4, 7, 13, 2, 1, 5, 9])

위와 같은 데이터가 있다고 가정해보자. 위 데이터 x의 평균을 경사하강법을 통해 찾아봅시다.

---

왜 평균인가?

평균은 "제곱 오차의 합"을 가장 작게 만드는 수 이기 때문에.

• 회귀분석의 핵심 아이디어도 여기서 나옵니다.
• 선형 회귀는 결국 예측값과 실제값의 차이 제곱의 합(=Loss) 을 줄이기 위한 작업입니다.
• 그래서 회귀에서도 항상 평균이 등장하고, 경사하강법도 이 원리를 따라 작동하게 됩니다.

---

모든 값과 어떤 수 B의 차이 제곱의 합을 최소화하면, 평균이 나옵니다.

def f(B):
    return np.sum((x - B) ** 2)

• 어떤 숫자들(예: [4, 7, 13, 2, 1, 5, 9])이 있을 때,
• 이 값들과의 거리(오차)를 제곱해서 다 더한 것을 최소로 만들고 싶을 때,
• "어디에 위치한 숫자 B를 선택해야 전체 거리 제곱의 합이 가장 작아질까?"

---

기울기(도함수) 정의

도함수란 무엇일까?

def f(x):
    return x ** 2

# x=2에서의 기울기 구하기
x = 2
h = 0.00001
slope = (f(x + h) - f(x)) / h
print(slope)  # 거의 4에 가까운 값이 나옴

즉, x에서 h만큼 이동했을 때의 변화율을 알려줍니다. (h는 아주 미세하다고 가정)
→ 이게 바로 경사하강법에서 ‘얼마나 움직일지’를 결정하는 핵심이 됩니다.

 

기울기 함수 만들기

x = np.array([4, 7, 13, 2, 1, 5, 9])  # 실제 데이터

# 손실 함수: B와의 차이 제곱합
def f(B):
    return np.sum((x - B) ** 2)

# 손실 함수의 도함수 (기울기)
def grad_f(B):
    return -2 * np.sum(x - B)

 

 

---

경사 하강법 사용

B = 0  # 시작 위치
learning_rate = 0.01  # 얼마나 움직일지
B_vals = []

for _ in range(50):  # 50번 반복
    B_vals.append(B)
    B -= learning_rate * grad_f(B)  # 기울기 방향의 반대로 이동!

 

왜 기울기의 반대로 이동할까?

 

• 시작점 x=3일 때 기울기 f′(3)=6 → 오르막이니까 왼쪽으로 이동
• 이동 후 x=1.2일 때 기울기 f′(1.2)=2.4 → 여전히 오르막, 계속 왼쪽
• 이렇게 기울기가 0에 가까워질수록 점점 이동량이 줄어들며 최솟값으로 수렴합니다.

 

"내려가고 싶으면, 오르막 방향의 반대로 가야 한다!"

 

경사 하강법 최종 코드

x = np.array([4, 7, 13, 2, 1, 5, 9])

# 목적 함수
def f(beta):
    return np.sum((x - beta) ** 2)

# 도함수 (기울기)
def grad_f(beta):
    return -2 * np.sum(x - beta)

# 경사하강법 실행
epochs = 50
lr = 0.01
B = 0.0
B_vals = []

for _ in range(epochs):
    B_vals.append(B)
    B -= lr * grad_f(B)

# 시각화
k = np.linspace(-1, 15, 200)
f_curve = np.array([f(b) for b in k])
f_vals = np.array([f(b) for b in B_vals])

plt.plot(k, f_curve, color='blue', label='f(B)')
plt.axvline(np.mean(x), color='red', linestyle='--', label=f'실제 평균: {np.mean(x):.2f}')
plt.plot(B_vals, f_vals, 'o--', color='orange', label='경사하강 경로')
plt.scatter(B_vals[-1], f_vals[-1], color='black', s=100, label='최종점')
plt.title('경사하강법 수렴 과정')
plt.xlabel('B')
plt.ylabel('f(B)')
plt.legend()
plt.grid(True)
plt.show()

 

결과 해석

• 그래프는 f(B) 곡선을 나타내고,
• 주황색 점들은 경사하강법이 움직인 경로를 나타냅니다.
• 빨간선은 실제 평균입니다.
• 마지막 검은 점은 경사하강법이 수렴한 지점, 즉 평균을 찾은 결과입니다.

👉 이렇게 수학적으로도 평균을 찾을 수 있다는 게 신기하죠?

---

5. 회귀분석과 경사하강법

우리가 데이터를 기반으로 회귀모형을 학습할 때,
오차제곱합(Mean Squared Error) 를 최소화하는 파라미터(기울기, 절편)를 찾는 게 핵심입니다.

즉, 다음과 같은 함수의 최소값을 찾는 문제로 변환되는 것입니다.

$$ J(\theta) = \sum (y_i - \hat{y}_i)^2 $$

이때, 기울기 계산 → 파라미터 업데이트 → 반복 과정을 수행하는 것이 바로 경사하강법입니다.

 

---

6. 추가 예제

• 등고선(Contour): 같은 함수 값을 갖는 지점을 선으로 연결한 것. 중심부로 갈수록 값이 작아집니다.
• 빨간 점 + 경로: 경사하강법이 이동한 경로 (초기값 → 최솟값으로 수렴)
• 검은 점: 최종 수렴 지점 → (x1,x2) = (0, 0.5)

 

파이썬 코드

# 함수 정의
def f(x1, x2):
    return 4 * x1**2 + 2 * (x2 - 0.5)**2

# 도함수 정의 (기울기)
def grad_f(x1, x2):
    return np.array([8 * x1, 4 * (x2 - 0.5)])

# 초기값, 학습률, 반복 횟수 설정
x = np.array([3.0, 3.0])
learning_rate = 0.01
epochs = 50000
path = [x.copy()]

# 경사하강법 수행
for _ in range(epochs):
    grad = grad_f(x[0], x[1])
    x -= learning_rate * grad
    path.append(x.copy())

path = np.array(path)

# 등고선 시각화용 데이터 생성
x1_vals = np.linspace(-3, 3, 400)
x2_vals = np.linspace(-1, 3, 400)
X1, X2 = np.meshgrid(x1_vals, x2_vals)
Z = f(X1, X2)

# 등고선 레벨 설정
levels = np.linspace(np.min(Z), np.max(Z), 15)

# 등고선 그래프
plt.figure(figsize=(8, 6))
contours = plt.contour(X1, X2, Z, levels=levels, cmap='viridis')
plt.clabel(contours, inline=True, fontsize=8, fmt="%.0f")

# 경사하강법 경로 표시
plt.plot(path[:, 0], path[:, 1], color='red', marker='o', markersize=3, label='경사하강법 경로')
plt.scatter(path[-1, 0], path[-1, 1], color='black', s=100, label='최종 수렴점')

# 그래프 설정
plt.title(r"$f(x_1, x_2) = 4x_1^2 + 2(x_2 - \frac{1}{2})^2$")
plt.xlabel("x1")
plt.ylabel("x2")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

# 최종 수렴 결과 출력
print(f"최종 수렴값: x1 = {path[-1, 0]:.4f}, x2 = {path[-1, 1]:.4f}")

 

---

7. 주의할 점

⚠️ 지역 최소값(Local Minima)이 2개 있는 함수

# 함수 정의
def f_local(x1, x2):
    return np.cos(x1) + (x2 - 1)**2

# 도함수 정의
def grad_f_local(x1, x2):
    return np.array([-np.sin(x1), 2 * (x2 - 1)])

# 초기값, 학습률, 반복 횟수
x = np.array([2.5, 3.0])
learning_rate = 0.05
epochs = 300
path_local = [x.copy()]

# 경사하강법 수행
for _ in range(epochs):
    grad = grad_f_local(x[0], x[1])
    x -= learning_rate * grad
    path_local.append(x.copy())

path_local = np.array(path_local)


# 시각화용 그리드 생성
x1_vals = np.linspace(-3, 3, 400)
x2_vals = np.linspace(-1, 3, 400)
X1, X2 = np.meshgrid(x1_vals, x2_vals)
Z_local = f_local(X1, X2)

# 등고선 레벨 설정
levels = np.linspace(np.min(Z_local), np.max(Z_local), 20)

# 시각화
plt.figure(figsize=(8, 6))
contours = plt.contour(X1, X2, Z_local, levels=levels, cmap='coolwarm')
plt.clabel(contours, inline=True, fontsize=8, fmt="%.2f")

# 경사하강법 경로
plt.plot(path_local[:, 0], path_local[:, 1], color='red', marker='o', markersize=3, label='경사하강법 경로')
plt.scatter(path_local[-1, 0], path_local[-1, 1], color='black', s=100, label='최종 수렴점')

# 설정
plt.title(r"$f(x_1, x_2) = \cos(x_1) + (x_2 - 1)^2$")
plt.xlabel("x1")
plt.ylabel("x2")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

# 최종 수렴값 출력
print(f"최종 수렴점: x1 = {path_local[-1, 0]:.4f}, x2 = {path_local[-1, 1]:.4f}")

• cos(x1​) 때문에 지역 최소값이 2개 존재합니다.

 

• 초기값이 (2.5, 3.0) 일 때의 결과입니다.
• 오른쪽에 있는 최소값에 수렴하고 있는 것을 볼 수 있습니다.

 

초기값을 한번 다양하게 설정해보겠습니다.

 

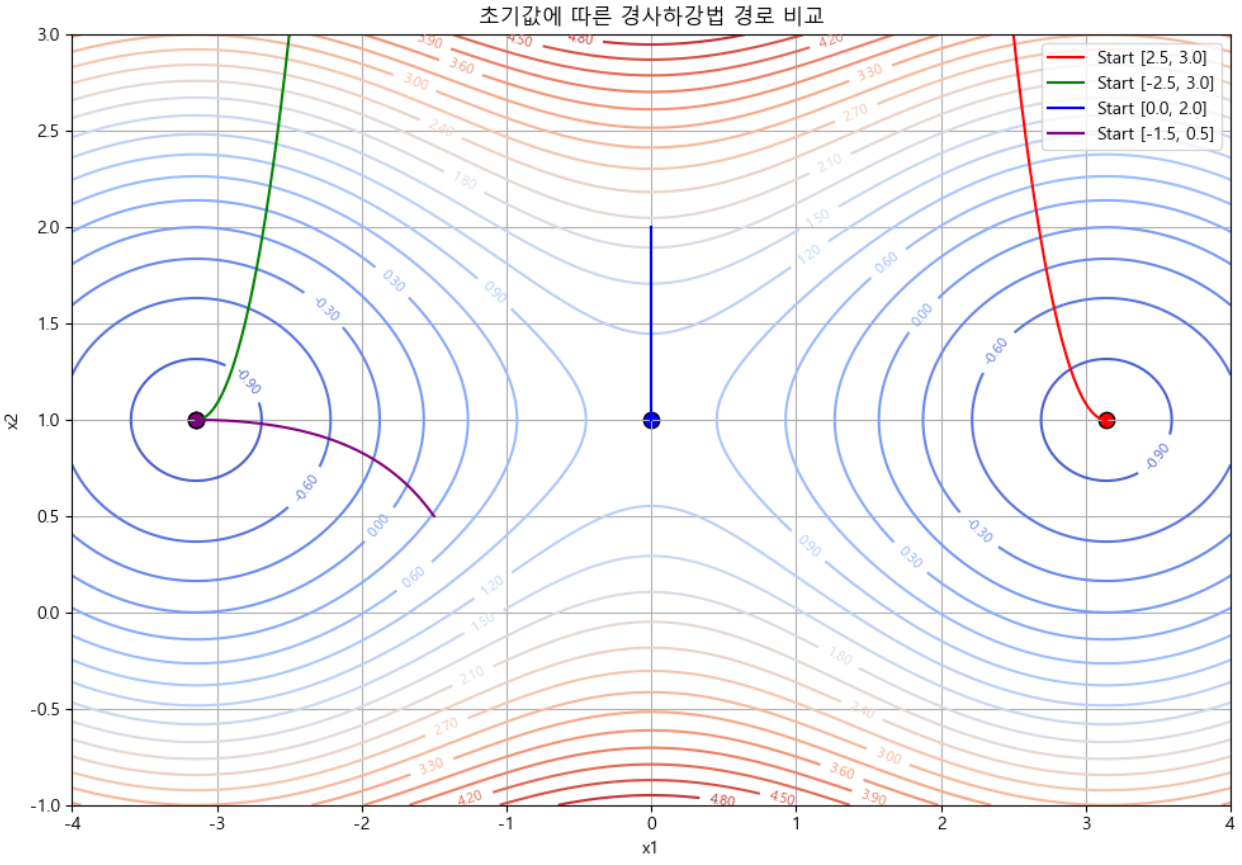
위 시각화 자료를 보면, 시작 위치에 따라 여러개의 최소값으로 수렴하고 있는 것을 볼 수 있습니다.

• 초기값 A: [2.5, 3.0] → x1​이 양수 → 오른쪽 골짜기에 수렴
• 초기값 B: [-2.5, 3.0] → x1​이 음수 → 왼쪽 골짜기에 수렴
• 이 둘은 모두 지역 최소값에 도달하지만, 전역 최소값은 아닐 수도 있습니다.

경사하강법은 근처에 있는 가장 낮은 점을 찾아나가기 때문입니다.

이로 인해, "지역 최소값(Local Minima)" 에 갇힐 수 있다는 문제가 발생할 수 있습니다.

---

지역 최소값이란?

지역 최소값이란, 함수의 국지적인 구간에서 가장 낮은 점이지만, 전체에서 가장 낮은 점은 아닌 지점을 의미합니다.

예를 들어, 다음과 같은 함수 $f(x_1, x_2) = \cos(x_1) + (x_2 - 1)^2$ 를 생각해봅시다.

이 함수는 다음과 같은 특징을 가집니다:

• x₁ 방향으로는 진동성(cos 함수)이 있어서 여러 개의 봉우리와 골짜기가 있습니다.
• x₂ 방향은 볼록한 포물선 모양이라 최소값이 분명합니다.

이 경우, 경사하강법은 시작점에 따라 서로 다른 골짜기(=지역 최소값)에 도착할 수 있습니다.

 

---

왜 문제가 되는가?

머신러닝에서는 손실 함수(loss function)가 복잡한 경우가 많습니다.
신경망의 경우 수천, 수만 개의 변수(가중치)가 얽혀 있기 때문에 함수의 모양도 복잡하고, 수많은 지역 최소값을 가질 수 있습니다.

이럴 때 경사하강법은 단 하나의 방향만 보고 이동하기 때문에,
더 나은 결과를 낼 수 있는 전역 최적점(Global Minimum) 을 발견하지 못하고 근처의 지역 최솟값에 멈춰버릴 수 있습니다.

---

다양한 해결 방법

방법	설명
여러 개의 초기값 사용	다양한 지점에서 시작해, 더 나은 최솟값을 선택
모멘텀(Momentum) 사용	이전 이동 방향을 반영해 관성처럼 이동
확률적 경사하강법(SGD)	샘플을 무작위로 선택해 노이즈를 넣음으로써 탈출 가능
학습률 감소(Learning rate decay)	초반엔 크게 이동하고 후반엔 작게 이동
고급 옵티마이저 사용 (Adam, RMSprop 등)	방향 보정 기능이 있는 최적화 알고리즘 사용

 

---

8. 정리

개념	설명
미분	기울기, 변화량을 측정하는 도구
도함수	미분된 함수. 그래프에서의 기울기를 나타냄
경사하강법	기울기를 따라 내려가며 함수의 최소값을 찾는 알고리즘
회귀 분석	데이터로부터 예측 모델(선형 관계 등)을 학습하는 방법
경사하강법과의 연결	오차를 줄이는 최적의 파라미터를 찾는 과정에 사용됨

• 경사하강법은 효율적이지만, 함수의 모양이 복잡할수록 '지역 최소값'에 갇힐 위험이 있습니다.
• 초기값, 함수 형태, 기울기 방향만 따르기 때문에 전역 최소값을 항상 보장하지 않습니다.
• 이를 방지하기 위해 다양한 전략과 기법이 함께 사용됩니다.